
Matematik başlı başına ilginc bir bilim dalı, cunku doğanın en kadim gizemlerine ışık tutuyor. Kimine gore zor kimine gore ise oldukca eğlenceli bir ders olan matematikte sıfır sayısının da ozel bir yeri var. Zira akıldan cıkmayan matematik kurallardan biri de bir sayıyı sıfıra bolemeyeceğinizdir.
Reel sayılarda, yani sayı doğrusundaki butun sayılar kumesinde bir sayının sıfır ile bolumu bize okullarda tanımsız diye oğretildi. Peki neden bir sayıyı sıfıra bolerseniz sonuc tanımsız olur hic merak ettiniz mi? Gelin isterseniz bu sorunun cevabına birlikte bakalım.
[h=2]Bir sayı neden 0'a bolunmez?[/h]
Herhangi bir reel sayının sıfıra bolumu tanımsızdır. Bolme işleminde sıfır ile bolum tanımlı değildir. Ayrıca sonsuz da değildir. Bolumun sonucu pozitif sonsuz ya da negatif sonsuz olabilir. İki sonsuz da bir reel sayı belirtmez, dolayısıyla kesin olarak soyleyebiliriz ki, sayı bolu sıfır tanımsızdır.
Mesela 10 sayısını sıfıra bolduğunuzde elinize ne gectiğini duşunmek icin; 10 ’u 5 ’e bolmekle başlayalım. Bu işlemin cevabı 2 olur. Peki ya 10 ’u daha ufak bir rakamla, 2 ’yle bolseydiniz ne olurdu? Daha buyuk bir sayı olan 5 ’i elde ederdiniz. Peki ya 10 ’un 1 ’e bolunmesi?

Yine daha buyuk bir rakam cıkar. 10. ½ ’ye bolunen 10, 20 eder. ¼ ’e bolunduğu zaman 40; 1/32 ’e bolunduğu zamansa 320 yapar. Ne zaman daha ufak bir sayıya bolseniz, karşılığında daha buyuk bir sayı elde edersiniz. Yani, bolen sayı 0 ’a ne kadar yaklaşırsa; cevabınız o kadar sonsuzluğa yaklaşır. Bu yuzden aslında 10 ’u 0 ’a bolseydiniz, sonsuzluk elde ederdiniz değil mi?
Bu işlemde bir sonuc almak adına yanlızca limit alabilirsiniz. (Sayı / X), x giderken sıfıra şeklinde ve bu fonksiyonun davranışını inceleyebilirsiniz. Ancak burada da karşımıza tek bir limit değeri cıkmaz, cunku limitler sağdan ve soldan farklıdır.Sıfıra sağdan yaklaşırken, fonksiyonun değeri pozitif olarak sonsuza doğru gider. Sonsuz bir kısaltmadır, anlamı ise, sonucun herhangi bir X reel sayısından yuksek olduğu, surekli buyuduğu ve dolayısıyla hicbir zaman belli olmadığıdır. Tek soyleyebileceğiniz, istediğiniz her reel sayıdan buyuk bir sonuc elde edebileceğinizdir.
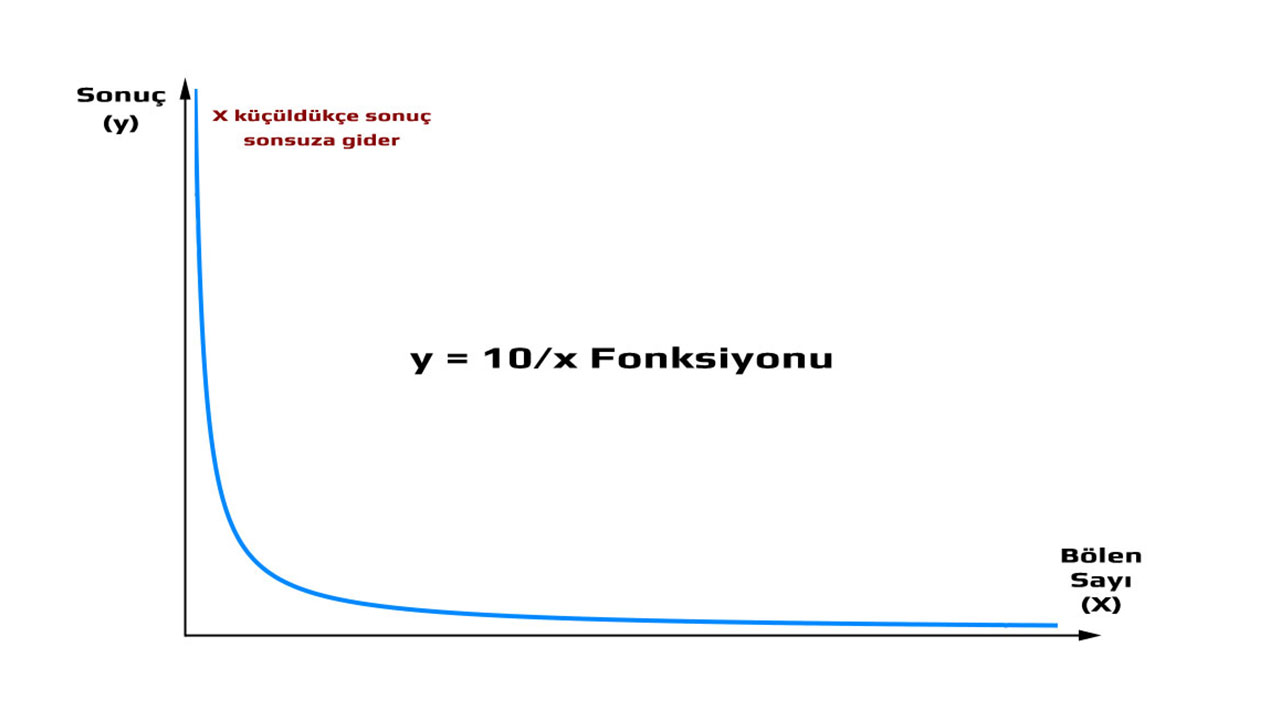
Sıfıra soldan yaklaşırken ise, durum negatif yonde aynıdır. Sayı mutlak değerce cok buyur ancak negatifdir, dolayısıyla kuculur. Belirleyebileceğiniz herhangi bir negatif reel sayıdan daha kucuk bir sayıdır, dolayısıyla eksi sonsuzdur denir. Soylediğimiz gibi, X/0'ın hicbir değeri yoktur, tanımlı bir işlem değildir. Sıfır ile asla bolme yapamazsınız.
Zaten sonsuz da reel sayılar kumesinde tanımlı bir sayı olmadığından, kesin olarak tanımsızdır. Sıfır bolu sıfır, bir uzeri sonsuz, sonsuz bolu sonsuz, sonsuz eksi sonsuz birer belirsizliktir. Tanımsız değildir. Bu işlemleri yapabilmek icin belirsizliğe neden olan durumu ortadan kaldırıp sonucu bulabiliriz.
Sıfıra bolme işlemi, yanıtını bulamadığınız bir işlemdir, bu nedenle işlemin sonucu tanımsızdır. Bolme ve carpmanın birbiriyle arasındaki ilişkiye bakacak olursak nedenini anlayabilirsiniz. 6'yı 3'e bolerseniz, cevap 2'dir, cunku 2 carpı 3 = 6 olur. 6'yı sıfıra bolerseniz, "Sıfır carpı 6'yı hangi sayı verir?" Sorusunu sorarsınız. Bunun cevabı elbette bir sayı değildir, cunku herhangi bir gercek sayının sıfır carpı sıfırın 6 olmadığını biliyoruz. Bu yuzden sıfıra bolmenin tanımsız olduğunu soyluyoruz, cunku diğer sayılarla bolme tutarlı değildir.
[h=2]Riemann Kuresi ve Stereografik Yansıtma[/h]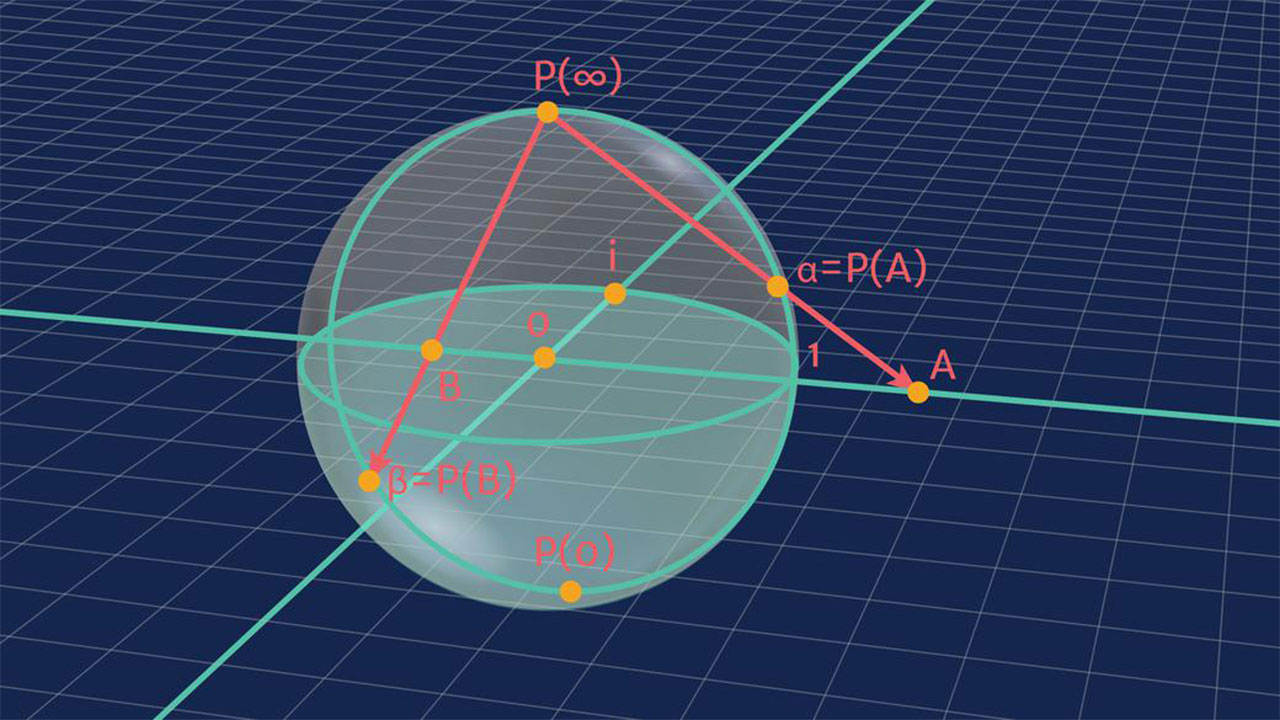
Duşunun ki, tum yonlerde sonsuzluğa giden ve ortada bir merkezi bulunmayan iki boyutlu bir duzlem var. Şimdi bu duzlemi bukup kureye cevirdiğinizi ve sıfırın guney kutbu olduğunu, koşelerin de en tepede; kuzey kutbu olan yerde birleştiğini hayal edin. Şimdi, bir başka sonsuz iki boyutlu duzlem alın ve onu ekvatoru kesecek şekilde yerleştirin. Bu duzlem uzerinde sectiğiniz herhangi bir nokta, kurenin Kuzey Kutbu ’na duz bir cizgiyle bağlanabilir. Eğer sectiğiniz nokta, kurenin dışındaysa; bağlantı cizgisi kureyle kuzey yarımkurede kesisecek. Eğer kurenin icerisindeyse, guney yarımkurede kesisecek.
Hayal ettiğiniz şey, bir Riemann Kuresi. Duzlemdeki her noktayı, kuredeki bir kesişim noktasıyla ilişkilendirmeyi kapsayan bu yonteme stereografik yansıtma deniyor. Temel olarak, duzlem uzerinde bulabileceğiniz herhangi bir noktayı kure uzerinde bulabilirsiniz. Buna sonsuzluk da dahil. Duzlemde sonsuzluğa ne kadar yaklaşırsanız, kurenin Kuzey Kutbu ’na da o kadar yaklaşırsınız.
[h=2]Başka bir ornekle acıklayacak olursak;[/h]
Portakallara elma eklerseniz ne olur? Elbette bir anlam ifade etmiyor, bu yuzden en kolay şey, mantıklı olmadığını veya bir matematikcinin dediği gibi, "tanımsız" olduğunu soylemektir. Belki de ona bakmanın en iyi yolu budur. Matematikte, "XYZ işlemi tanımsız" gibi bir ifade gorduğunuzde, bunu kafanızda "XYZ işlemi bir anlam ifade etmiyor" şeklinde duşunebilirsiniz.
Bunu duşunmenin başka bir yolu da bir kutuyu elmalarla doldurmayı hayal etmektir. Bir kutuda 100 elma olduğunu varsayalım. Şimdi bu elmaların yarısı buyukluğundeki elmalarla doldurmayı deneyin. Kutuya 200 tane elma koyabilirsiniz. Şimdi hic yer kaplamayan ozel, sihirli bir elma hayal edin. Kutuya kac tane koyabilirsiniz?
Bu işlemin herhangi bir cevabı yok. Bu nedenle matematikciler 0'a bolunen sayıları "tanımsız" olarak adlandırır. Bazı araştırmacılar bu işlemi sonsuz olarak gorme eğilimindedir, ancak bu işlem tam olarak doğru değildir. Oncelikle bir sayının sıfıra bolumu ilk bakışta sonsuz gibi duşunulebilir. Cunku bolen sayı kuculdukce sonuc buyur. Orneğin 10 sayısını her adımda daha kucuk sayılara bolersek sonucun buyuduğunu goruruz.
10 / Bolen Sayı = Sonuc 10 / 1 = 10 10 / 0,1 = 100 10 / 0,01 = 1000 10 / 0,001 = 10000 10 / 0,0001 = 100000 10 / 0,00001 = 1000000 10 / 0,000001 = 10000000 Bağıntı = 10/x = y Gorduğunuz gibi bolen sayı ne kadar kucuk olursa sonuc o kadar buyuk olmaktadır. Yani bolen sayı sıfıra yaklaştıkca sonuc da sonsuza yaklaşmaktadır. O halde bir sayının sıfıra bolumu sonsuz olmalıdır.

Bu durumun neden doğru olmadığını anlamak icin oncelikle bolme işleminin ne ifade ettiğini bilmemiz gerekir. Orneğin 10 sayısını 2 sayısına bolduğumuzde sonuc 5 cıkar. Bu işlem bize 10'un icinde kac tane 2 olduğunu gosterir. Ayrıca bolme işlemi matematiksel olarak carpma işleminin tersidir. Bolme ve carpma işlemlerinin sonucunu birbirine eşit olacak şekilde duzenlersek carpımsal ters kavramı ortaya cıkar.
10 / 5 = 2 = 10 x 1/5 10 / 2 = 5 = 10 x 1/2 10/a = 10 x 1/a İşlemlerdeki 1/a sayısına carpımsal ters denir. ilk işlemde 5'in carpımsal tersi 1/5, ikinci işlemde 2'nin carpımsal tersi 1/2'dir. Yani bir sayının carpımsal tersi 1'in bu sayıya bolumudur (a'nın carpımsal tersi 1/a 'dır). Peki carpımsal ters ne işimize yarayacak? Bir sayının carpımsal tersi ile carpımı daima 1 sonucunu verir.
Sayı x Carpımsal Ters = 1 5 x 1/5 =1 2 x 1/2 = 1 4000 x 1/4000 = 1 a x 1/a = 1 Bu durumda sıfırın carpımsal tersi 1/0 olmalı ve carpımsal tersi ile carpımı da 1'i vermelidir (0 x 1/0 = 1). İşte sorun burada ortaya cıkar. Cunku bir sayının sıfır ile carpımı sıfırdır. Bu nedenle sıfırın carpımsal tersi yoktur. Yani 1/0 tanımsızdır. Sayıların sıfıra bolum işlemlerini carpım olarak yazarsak
5/0 = 5 x 1/0 10/0 = 10 x 1/0 -3/0 = -3 x 1/0 1/0 tanımsız olduğu icin butun sonuclar tanımsızdır. Yani bir sayının sıfıra bolumu tanımsızdır. İlk kısımda bahsettiğim ve mantıklı gibi gorunen 1/0 = Sonsuz duşuncesi hala mantıklı gibi gelebilir. Fakat bu durum negatif sayılar icin de aynı sonucu vermektedir. Bir sayıyı sıfıra yaklaşan negatif sayılara bolduğumuzde sonuc eksi sonsuza yaklaşır.

10 / Negatif Bolen Sayı = Sonuc 10 / -1 = -10 10 / -0,1 = -100 10 / -0,01 = -1000 10 / -0,001 = -10000 10 / -0,0001 = -100000 10 /- 0,00001 = -1000000 10 /- 0,000001 = -10000000 Bağıntı = 10/-x = -y Bu nedenle 1/0 sonucu sonsuz ise 1/-0 sonucu da eksi sonsuz olmalıdır. Sıfır notr bir sayı olduğundan 1/0 icin hem artı sonsuz hem de eksi sonsuz sonucları ortaya cıkar. Artı sonsuz ile eksi sonsuz birbirine eşit olmadığından bu duşuncenin yanlış olduğu gorulur.
Butun bu işlemler kafanızı karıştırdıysa basit bir mantık uzerinden gidelim. Onceki kısımlarda bahsettiğim gibi orneğin 10/5 işlemi 10'un icinde kac tane 5 olduğunu gosterir. Buna gore 10/0 işlemi 10'nun icinde kac tane sıfır olduğunu gostermelidir. 10'un icinde kac tane sıfır vardır? 1, 10, sonsuz... bilmiyoruz cunku sonuc matematiksel olarak tanımlanmamıştır. Bu nedenle bir sayıyı sıfıra bolersek sonuc tanımsızdır.
Bu yazımızda sizlerle bir sayının neden sıfıra bolunemediğini tum detaylarıyla acıklamaya calıştık. Meraklıları icin faydalı olduğunu duşunduğumuz bu yazıda, bir sayıyı sıfıra bolduğumuzde neler olur, sonuc tanımsız mı yoksa sonsuz mu sorularına yanıt aradık. Bir sonraki yazımızda buluşuncaya dek sağlıcakla kalın.
Reel sayılarda, yani sayı doğrusundaki butun sayılar kumesinde bir sayının sıfır ile bolumu bize okullarda tanımsız diye oğretildi. Peki neden bir sayıyı sıfıra bolerseniz sonuc tanımsız olur hic merak ettiniz mi? Gelin isterseniz bu sorunun cevabına birlikte bakalım.
[h=2]Bir sayı neden 0'a bolunmez?[/h]

Herhangi bir reel sayının sıfıra bolumu tanımsızdır. Bolme işleminde sıfır ile bolum tanımlı değildir. Ayrıca sonsuz da değildir. Bolumun sonucu pozitif sonsuz ya da negatif sonsuz olabilir. İki sonsuz da bir reel sayı belirtmez, dolayısıyla kesin olarak soyleyebiliriz ki, sayı bolu sıfır tanımsızdır.
Mesela 10 sayısını sıfıra bolduğunuzde elinize ne gectiğini duşunmek icin; 10 ’u 5 ’e bolmekle başlayalım. Bu işlemin cevabı 2 olur. Peki ya 10 ’u daha ufak bir rakamla, 2 ’yle bolseydiniz ne olurdu? Daha buyuk bir sayı olan 5 ’i elde ederdiniz. Peki ya 10 ’un 1 ’e bolunmesi?

Yine daha buyuk bir rakam cıkar. 10. ½ ’ye bolunen 10, 20 eder. ¼ ’e bolunduğu zaman 40; 1/32 ’e bolunduğu zamansa 320 yapar. Ne zaman daha ufak bir sayıya bolseniz, karşılığında daha buyuk bir sayı elde edersiniz. Yani, bolen sayı 0 ’a ne kadar yaklaşırsa; cevabınız o kadar sonsuzluğa yaklaşır. Bu yuzden aslında 10 ’u 0 ’a bolseydiniz, sonsuzluk elde ederdiniz değil mi?
Bu işlemde bir sonuc almak adına yanlızca limit alabilirsiniz. (Sayı / X), x giderken sıfıra şeklinde ve bu fonksiyonun davranışını inceleyebilirsiniz. Ancak burada da karşımıza tek bir limit değeri cıkmaz, cunku limitler sağdan ve soldan farklıdır.Sıfıra sağdan yaklaşırken, fonksiyonun değeri pozitif olarak sonsuza doğru gider. Sonsuz bir kısaltmadır, anlamı ise, sonucun herhangi bir X reel sayısından yuksek olduğu, surekli buyuduğu ve dolayısıyla hicbir zaman belli olmadığıdır. Tek soyleyebileceğiniz, istediğiniz her reel sayıdan buyuk bir sonuc elde edebileceğinizdir.

Sıfıra soldan yaklaşırken ise, durum negatif yonde aynıdır. Sayı mutlak değerce cok buyur ancak negatifdir, dolayısıyla kuculur. Belirleyebileceğiniz herhangi bir negatif reel sayıdan daha kucuk bir sayıdır, dolayısıyla eksi sonsuzdur denir. Soylediğimiz gibi, X/0'ın hicbir değeri yoktur, tanımlı bir işlem değildir. Sıfır ile asla bolme yapamazsınız.
Zaten sonsuz da reel sayılar kumesinde tanımlı bir sayı olmadığından, kesin olarak tanımsızdır. Sıfır bolu sıfır, bir uzeri sonsuz, sonsuz bolu sonsuz, sonsuz eksi sonsuz birer belirsizliktir. Tanımsız değildir. Bu işlemleri yapabilmek icin belirsizliğe neden olan durumu ortadan kaldırıp sonucu bulabiliriz.
Sıfıra bolme işlemi, yanıtını bulamadığınız bir işlemdir, bu nedenle işlemin sonucu tanımsızdır. Bolme ve carpmanın birbiriyle arasındaki ilişkiye bakacak olursak nedenini anlayabilirsiniz. 6'yı 3'e bolerseniz, cevap 2'dir, cunku 2 carpı 3 = 6 olur. 6'yı sıfıra bolerseniz, "Sıfır carpı 6'yı hangi sayı verir?" Sorusunu sorarsınız. Bunun cevabı elbette bir sayı değildir, cunku herhangi bir gercek sayının sıfır carpı sıfırın 6 olmadığını biliyoruz. Bu yuzden sıfıra bolmenin tanımsız olduğunu soyluyoruz, cunku diğer sayılarla bolme tutarlı değildir.
[h=2]Riemann Kuresi ve Stereografik Yansıtma[/h]

Duşunun ki, tum yonlerde sonsuzluğa giden ve ortada bir merkezi bulunmayan iki boyutlu bir duzlem var. Şimdi bu duzlemi bukup kureye cevirdiğinizi ve sıfırın guney kutbu olduğunu, koşelerin de en tepede; kuzey kutbu olan yerde birleştiğini hayal edin. Şimdi, bir başka sonsuz iki boyutlu duzlem alın ve onu ekvatoru kesecek şekilde yerleştirin. Bu duzlem uzerinde sectiğiniz herhangi bir nokta, kurenin Kuzey Kutbu ’na duz bir cizgiyle bağlanabilir. Eğer sectiğiniz nokta, kurenin dışındaysa; bağlantı cizgisi kureyle kuzey yarımkurede kesisecek. Eğer kurenin icerisindeyse, guney yarımkurede kesisecek.
Hayal ettiğiniz şey, bir Riemann Kuresi. Duzlemdeki her noktayı, kuredeki bir kesişim noktasıyla ilişkilendirmeyi kapsayan bu yonteme stereografik yansıtma deniyor. Temel olarak, duzlem uzerinde bulabileceğiniz herhangi bir noktayı kure uzerinde bulabilirsiniz. Buna sonsuzluk da dahil. Duzlemde sonsuzluğa ne kadar yaklaşırsanız, kurenin Kuzey Kutbu ’na da o kadar yaklaşırsınız.
[h=2]Başka bir ornekle acıklayacak olursak;[/h]

Portakallara elma eklerseniz ne olur? Elbette bir anlam ifade etmiyor, bu yuzden en kolay şey, mantıklı olmadığını veya bir matematikcinin dediği gibi, "tanımsız" olduğunu soylemektir. Belki de ona bakmanın en iyi yolu budur. Matematikte, "XYZ işlemi tanımsız" gibi bir ifade gorduğunuzde, bunu kafanızda "XYZ işlemi bir anlam ifade etmiyor" şeklinde duşunebilirsiniz.
Bunu duşunmenin başka bir yolu da bir kutuyu elmalarla doldurmayı hayal etmektir. Bir kutuda 100 elma olduğunu varsayalım. Şimdi bu elmaların yarısı buyukluğundeki elmalarla doldurmayı deneyin. Kutuya 200 tane elma koyabilirsiniz. Şimdi hic yer kaplamayan ozel, sihirli bir elma hayal edin. Kutuya kac tane koyabilirsiniz?
Bu işlemin herhangi bir cevabı yok. Bu nedenle matematikciler 0'a bolunen sayıları "tanımsız" olarak adlandırır. Bazı araştırmacılar bu işlemi sonsuz olarak gorme eğilimindedir, ancak bu işlem tam olarak doğru değildir. Oncelikle bir sayının sıfıra bolumu ilk bakışta sonsuz gibi duşunulebilir. Cunku bolen sayı kuculdukce sonuc buyur. Orneğin 10 sayısını her adımda daha kucuk sayılara bolersek sonucun buyuduğunu goruruz.
10 / Bolen Sayı = Sonuc 10 / 1 = 10 10 / 0,1 = 100 10 / 0,01 = 1000 10 / 0,001 = 10000 10 / 0,0001 = 100000 10 / 0,00001 = 1000000 10 / 0,000001 = 10000000 Bağıntı = 10/x = y Gorduğunuz gibi bolen sayı ne kadar kucuk olursa sonuc o kadar buyuk olmaktadır. Yani bolen sayı sıfıra yaklaştıkca sonuc da sonsuza yaklaşmaktadır. O halde bir sayının sıfıra bolumu sonsuz olmalıdır.

Bu durumun neden doğru olmadığını anlamak icin oncelikle bolme işleminin ne ifade ettiğini bilmemiz gerekir. Orneğin 10 sayısını 2 sayısına bolduğumuzde sonuc 5 cıkar. Bu işlem bize 10'un icinde kac tane 2 olduğunu gosterir. Ayrıca bolme işlemi matematiksel olarak carpma işleminin tersidir. Bolme ve carpma işlemlerinin sonucunu birbirine eşit olacak şekilde duzenlersek carpımsal ters kavramı ortaya cıkar.
10 / 5 = 2 = 10 x 1/5 10 / 2 = 5 = 10 x 1/2 10/a = 10 x 1/a İşlemlerdeki 1/a sayısına carpımsal ters denir. ilk işlemde 5'in carpımsal tersi 1/5, ikinci işlemde 2'nin carpımsal tersi 1/2'dir. Yani bir sayının carpımsal tersi 1'in bu sayıya bolumudur (a'nın carpımsal tersi 1/a 'dır). Peki carpımsal ters ne işimize yarayacak? Bir sayının carpımsal tersi ile carpımı daima 1 sonucunu verir.
Sayı x Carpımsal Ters = 1 5 x 1/5 =1 2 x 1/2 = 1 4000 x 1/4000 = 1 a x 1/a = 1 Bu durumda sıfırın carpımsal tersi 1/0 olmalı ve carpımsal tersi ile carpımı da 1'i vermelidir (0 x 1/0 = 1). İşte sorun burada ortaya cıkar. Cunku bir sayının sıfır ile carpımı sıfırdır. Bu nedenle sıfırın carpımsal tersi yoktur. Yani 1/0 tanımsızdır. Sayıların sıfıra bolum işlemlerini carpım olarak yazarsak
5/0 = 5 x 1/0 10/0 = 10 x 1/0 -3/0 = -3 x 1/0 1/0 tanımsız olduğu icin butun sonuclar tanımsızdır. Yani bir sayının sıfıra bolumu tanımsızdır. İlk kısımda bahsettiğim ve mantıklı gibi gorunen 1/0 = Sonsuz duşuncesi hala mantıklı gibi gelebilir. Fakat bu durum negatif sayılar icin de aynı sonucu vermektedir. Bir sayıyı sıfıra yaklaşan negatif sayılara bolduğumuzde sonuc eksi sonsuza yaklaşır.

10 / Negatif Bolen Sayı = Sonuc 10 / -1 = -10 10 / -0,1 = -100 10 / -0,01 = -1000 10 / -0,001 = -10000 10 / -0,0001 = -100000 10 /- 0,00001 = -1000000 10 /- 0,000001 = -10000000 Bağıntı = 10/-x = -y Bu nedenle 1/0 sonucu sonsuz ise 1/-0 sonucu da eksi sonsuz olmalıdır. Sıfır notr bir sayı olduğundan 1/0 icin hem artı sonsuz hem de eksi sonsuz sonucları ortaya cıkar. Artı sonsuz ile eksi sonsuz birbirine eşit olmadığından bu duşuncenin yanlış olduğu gorulur.
Butun bu işlemler kafanızı karıştırdıysa basit bir mantık uzerinden gidelim. Onceki kısımlarda bahsettiğim gibi orneğin 10/5 işlemi 10'un icinde kac tane 5 olduğunu gosterir. Buna gore 10/0 işlemi 10'nun icinde kac tane sıfır olduğunu gostermelidir. 10'un icinde kac tane sıfır vardır? 1, 10, sonsuz... bilmiyoruz cunku sonuc matematiksel olarak tanımlanmamıştır. Bu nedenle bir sayıyı sıfıra bolersek sonuc tanımsızdır.
Bu yazımızda sizlerle bir sayının neden sıfıra bolunemediğini tum detaylarıyla acıklamaya calıştık. Meraklıları icin faydalı olduğunu duşunduğumuz bu yazıda, bir sayıyı sıfıra bolduğumuzde neler olur, sonuc tanımsız mı yoksa sonsuz mu sorularına yanıt aradık. Bir sonraki yazımızda buluşuncaya dek sağlıcakla kalın.